Ring Bank Theory of Conscious Semiosis:
Baseline Dynamics and Aboutness Modulation

1 Introduction

RBT treats conscious experience as semiosis in motion. Instead of beginning with content, RBT begins with when and where access happens, and lets what (paint/semantics) be the downstream consequence. We articulate three organizing claims:

1. Access-first geometry. Conscious sampling occurs on a dynamic, low-dimensional Access Manifold $\A(t)$ embedded in a posed Bank $\B$ (a shape manifold under $\Sim(3)$). A printing operator $\Pi$ writes ringframes $\rho(t)$ that populate a fading Time Schema $\T$.
2. Baseline vs. aboutness. A slow baseline sets macro-cadence and bank behavior; aboutness modulation steers pose, intra-bank walks, and timing so that access meets the currently relevant object of thought or action.
3. Semiosis as cascade. A Peircean-style three-stage cascade links mic/baseline driven prints (representamina) to $\R/\I$ readouts (interpretants) and then to threats/affordances and action (objects) [6]. Aboutness is sometimes controlled, often modulated.

This paper consolidates prior drafts into a self-consistent formalization, gives precise operational definitions for modes of printing, and outlines falsifiable predictions aligned with neural observations in dissociation/hyperpolarization and task-related dynamics [7-11].

2 Core Objects

2.1 Bank ($\B$): 3D Shape Space with $\Sim(3)$ Action

In plain terms, the Bank is largely a cube/sphere agglomerated object, with hundreds of concentric copies scaling inwards. In reality, every shape you model stores lightly upon it. Let $\mathcal{S}$ denote a shape space of configurations modulo translation, rotation, and scale (Kendall-type shape space). The Bank $\B$ could be thought of as a single, extremely complex shape, and as such, could be considered a latent point (or submanifold) $S\in\mathcal{S}$ encoding perspective-invariant relational geometry (compare Lehar's concentric scaffolds [3,4]). A conscious display chooses a pose $g(t)\in\Sim(3)$ acting on a canonical representative:

Content and context (aboutness, discussed in greater precision later as modulating up to all variables of conscious rendering jointly) can restrict $g(t)$ to a coset $g(t)H$ where $H$ stabilizes $S$ (symmetries). This separation of shape (what) and pose (where/how big) makes attitude misalignment precise: e.g., a yaw error is a systematic rotation in $R(t)$ between body- and environment-subspaces (cf. grasp underreach anecdote).

2.2 Real Schema ($\R$): 3D Veridical World Model for Action

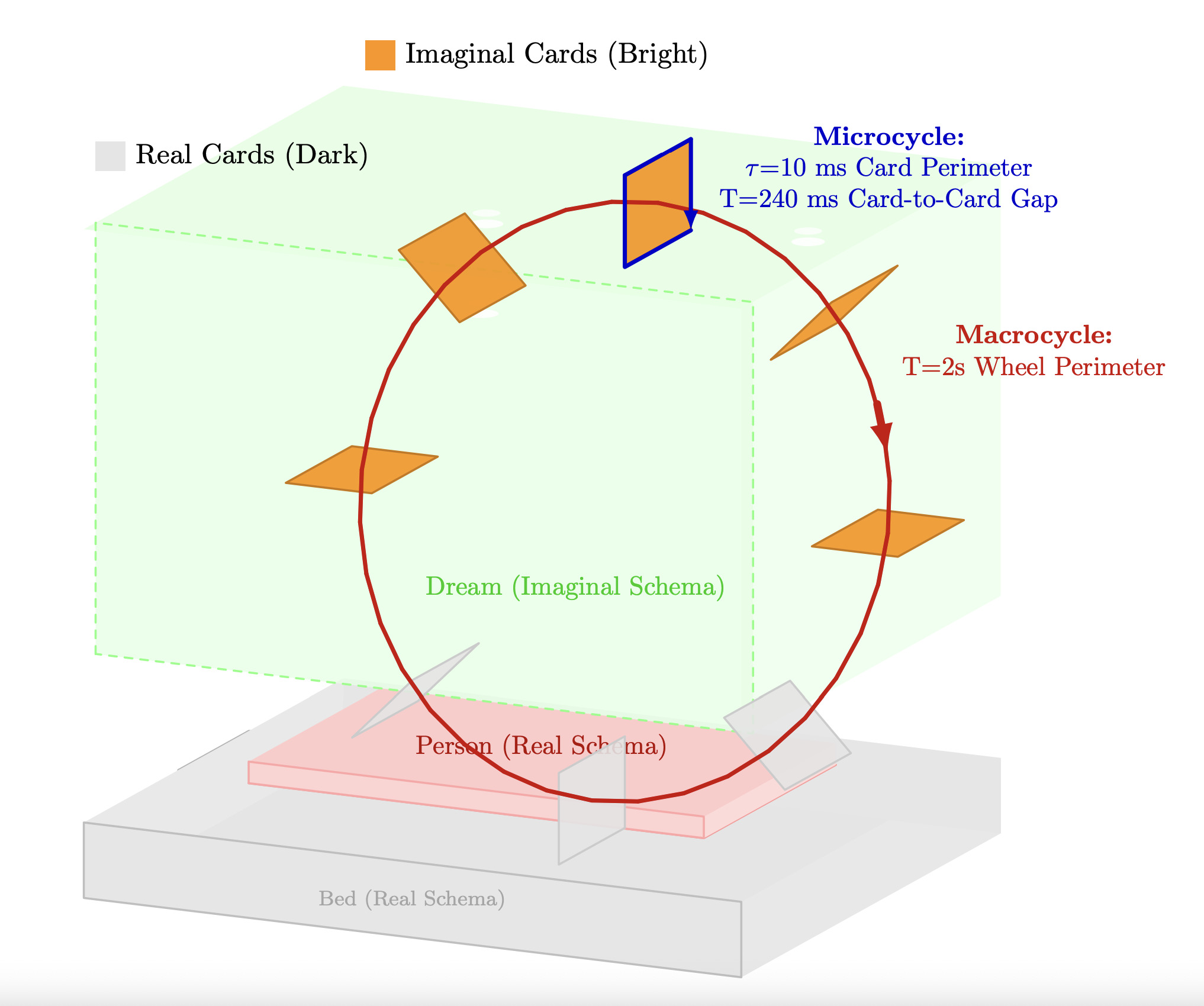
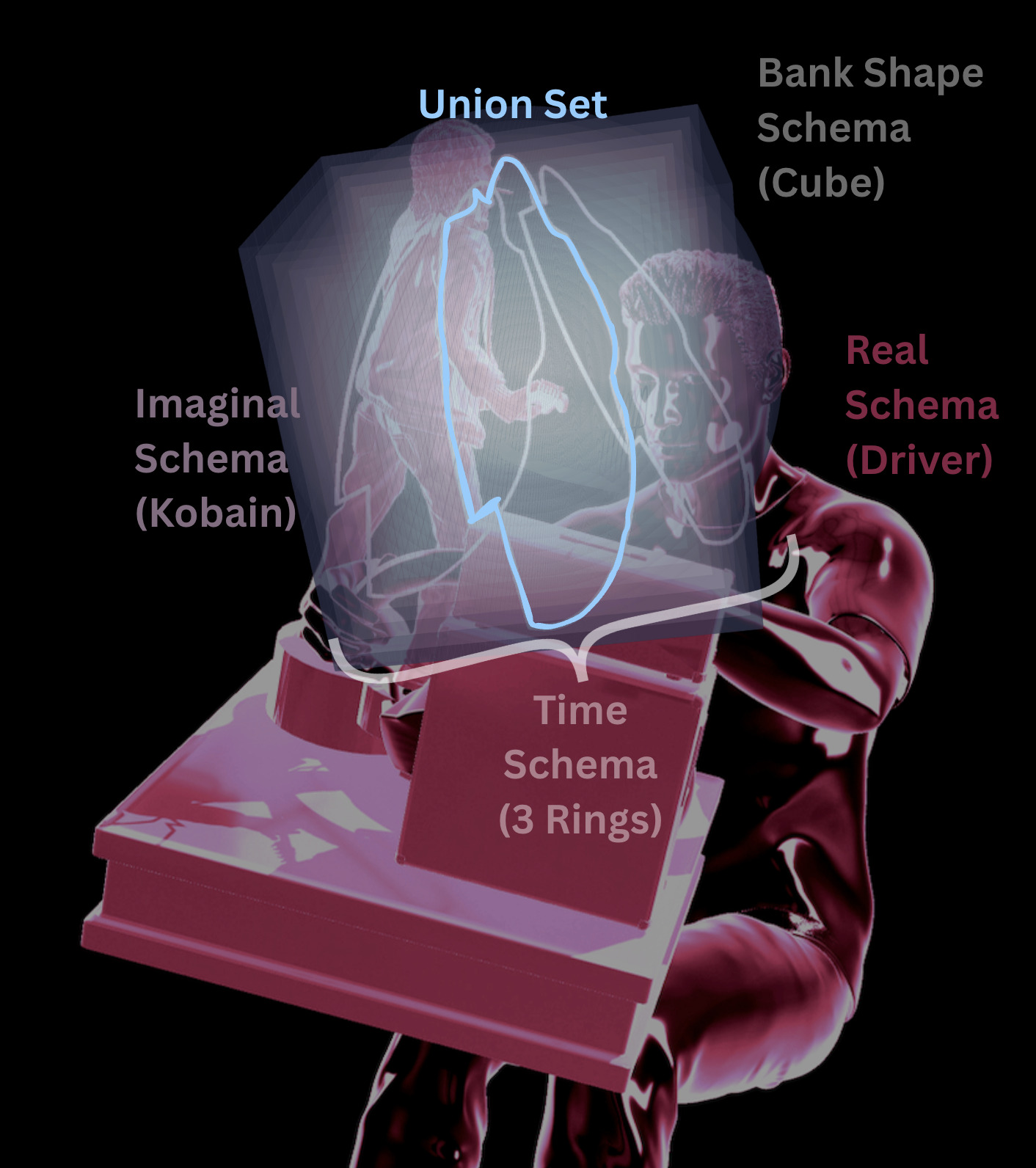
The real schema $\R$ is the 3D understanding of the immediate world that guides the body schema and physical movement. It consists of:

• Stereo geometry: Left-eye and right-eye volumes merged into a cyclopean view behind the nose via rotation around the focal object
• Hierarchical structure: Nested schemas including body, environment, and key object representations
• Dual temporal modes: Both static (present snapshot) and dynamic (changing world) representations

As the servo target for physical action, $\R$ provides the spatial framework for avatar movement and real-world interaction. Movement errors often arise from attitude misalignment between the body schema and the visually-derived environment schema (the two main components of $\R$). For example, a yaw error in the body schema—where it is assumed to be rotated slightly clockwise (bird's-eye view) from its actual position relative to the visually perceived refrigerator—results in an underreach when grasping the handle. The arm is miscalculated as being closer to the target than it actually is, despite correct trajectory planning.

2.3 Imaginal Schema ($\I$): 3D Non-Veridical Workspace with Sim(3) Action

The imaginal schema $\I$ provides a dynamic volumetric overlay to the real schema $\R$, serving as a workspace for non-veridical spatial representation and reasoning. Key properties include:

• Functional scope: Generates hypothetical situations, warning imagery (e.g., potential bitten-finger flash when bringing fingers into mouth while eating chips to induce caution), memories, conceptual contemplation, action simulations, and dream content,
• Viewing perspective: Typically observed by a "mind's eye" that can orbit and relocate (and $\I$ itself can rapidly zoom) independently of the avatar's cyclopean eye in $\R$, though dreams and certain cases may embed a "mind's avatar" within $\I$,
• Dynamic interaction: Frequent switching between $\R$ and $\I$ occurs during normal cognition, with $\I$ serving as a temporary workspace before returning to reality-based processing,
• Display dominance: While often overlaying $\R$, $\I$ can fully dominate conscious frames, creating anticorrelated periods of purely imaginal or real experience,
• Volumetric scaling: Objects are dynamically rescaled relative to $\R$ with extreme rapidity—comparable to the fastest camera zoom—frequently enlarging small elements for detailed inspection,
• Variable visibility: Ranges from completely transparent to vivid and photorealistic, with individual differences in conscious access—some experience $\I$ as plain as day while others have little visual awareness,
• Non-veridical content: Supports imagined, remembered, or potential future geometries—places, times, and scenarios not matching to $\R$,
• Geometric utility: Maintains full spatial functionality regardless of visibility, enabling both conscious inspection and "blindsight"-style geometric processing.

Unlike the action-oriented $\R$, $\I$ serves as a flexible workspace where metacognition operates as observer of non-literal geometric content. It is possible to have more than one $\I$ at once.

2.4 Time Schema ($\T$): 3D Flowfield and Fading Buffer with Sim(3) Action

$\T$ stores recent prints as a fading temporal stack, producing the illusion of continuity via overlap of access windows:

• Ringframe sequencing: fading history of recent $\rho(\tau)$ over $\tau\in[t-\Delta,t]$ yields continuity.
• Multi-modal timing: supports both continuous phasic scanning and discrete interrupts.
• Dynamic cadence: governed by competition between baseline rhythm $\beta(t)$ and mic events.

Conscious "printing" is the act of the operator $\Pi$ sampling on $\A$:

$\T$ functions as a fading stack or flowfield of recent $\rho$ printed by $\Pi$ on $\A$, yielding apparent continuity from discrete acts of access. The activity of $\Pi$ may follow either of two drives: a transient, high-level mic signal $\M(t)$ conveying structured content, or an endogenous baseline rhythm $\beta(t)$ maintained by refractory dynamics when $\M(t)$ is silent. Thus,

Phasic modes correspond to continuous modulation of $\beta(t)$ by $\M(t)$, whereas interrupt modes reflect discrete, hazard-scheduled prints. Both contribute to the ongoing flowfield of $\T$, which merges the outputs of $\Pi$ into a seemingly continuous conscious stream.

2.5 Real $\R$ and Imaginal $\I$ are Readouts with Latency

We treat $\R$ (veridical, action-oriented) and $\I$ (non-veridical, constructive) as readouts integrating recent prints:

with a causal kernel $G$. Vividness and rapid zooms reflect gain and $\Sim(3)$ pose control over IT/PPC codes. $\I$ may overlay or dominate $\R$.

2.6 Access Manifold ($\A$, 0–2D) and Display ($\D$ (=$\Ustruct$))

We distinguish the structural union (full conscious display, union of schemas on manifold)

from the operational access manifold (intersection of schemas)

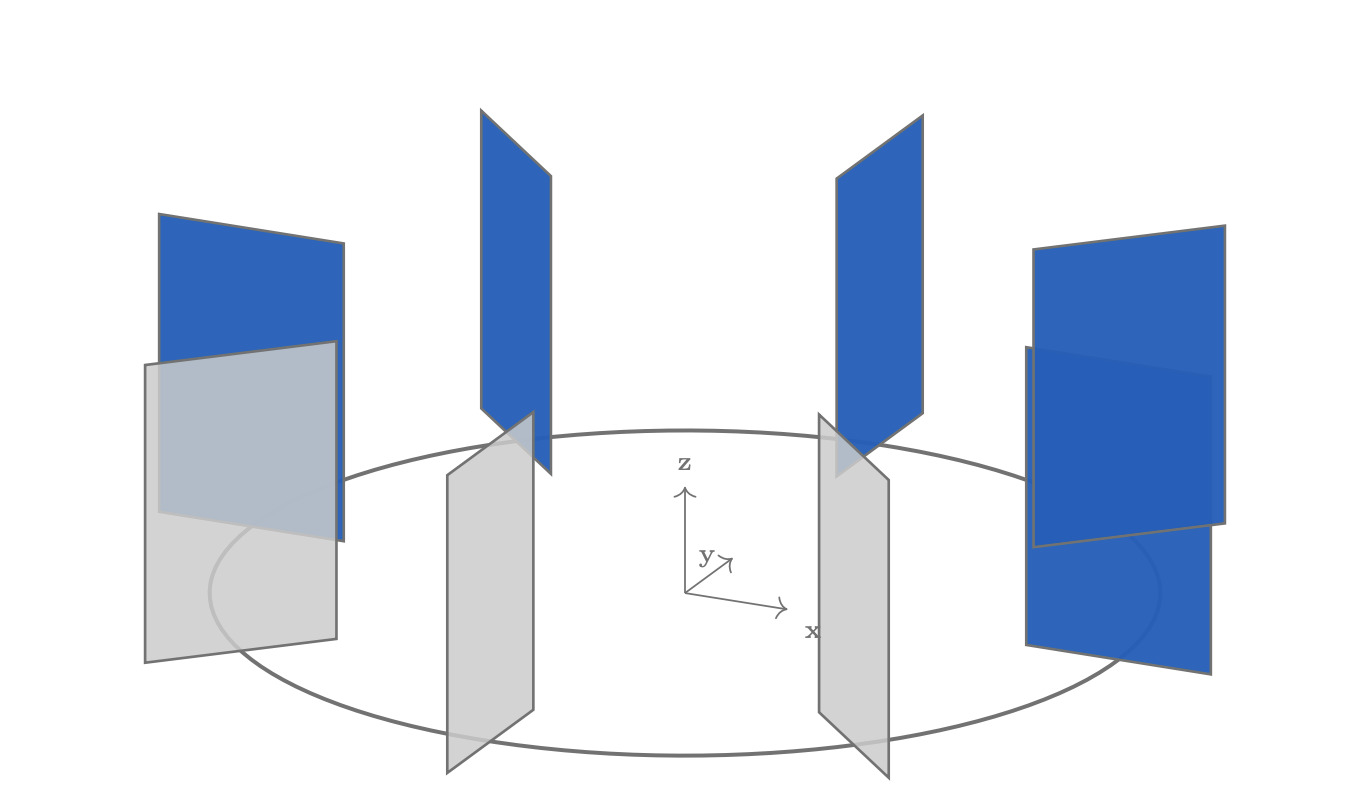
which is the locus where conscious sampling may occur "now." $\Ustruct$ is everything in the display; $\A$ is what is touched between schemas—a subset of $\B$ that often exhibits a graded excitability or printing potential, sometimes spreading radially from a central focus outward across the bank.

2.7 Ringframes ($\rho$): 0–2D Fading Manifolds

A ringframe $\rho(t)$ is material printed by the operator $\Pi$ on the access manifold $\A$ into the time schema $\T$. It is the basic unit of conscious access, bridging $\B \rightarrow \A \rightarrow \T$.

• Ring: 0–1D print — a tracer following a path or the instantaneous print of that path.
• Frame: 2D print — access activity that sweeps or fills an area of $\A$ over time, whether all at once or by motion.

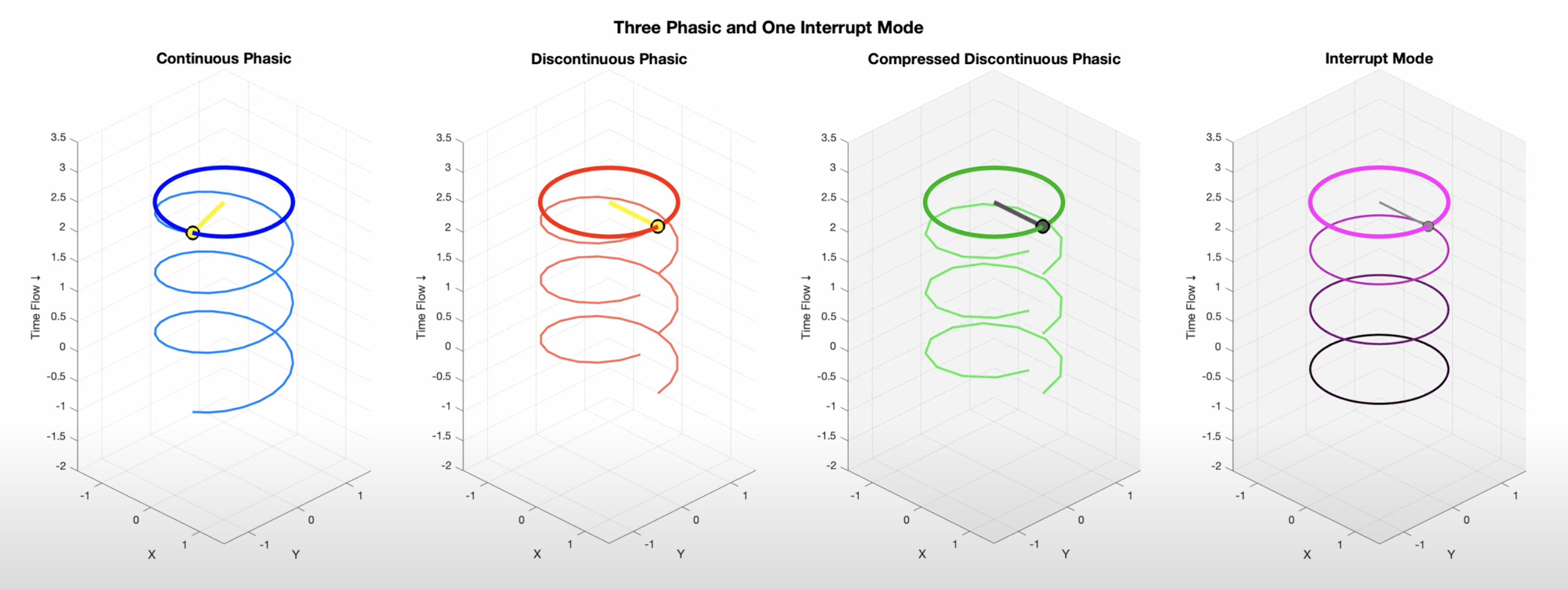
Both are printed from the Bank $\B$, posed by $g(t)\in\Sim(3)$, and deposited in $\T$ as a record. Phasic modes yield seamless cycles (helices in $\T$), compressed phasic modes yield lock-washer type geometries in $\T$, and interrupt modes produce discrete frames in $\T$. Square trajectories; swept or extruded contours; unclosed V, U or linear manifolds (as trajectories or swept contours); etc.; are all still considered ringframe material, since they arise from the same act of printing by $\Pi$ on $\A$ into $\T$. As hippocampal patients retain immediate present context, it is not thought that the time schema/ringframes are instantiated by the HPC, although the greater HPC (including EC), RSP, and DMN (including ACC/mPFC) might be at play.

2.8 Printing Operator ($\Pi$): Sampling the Access Manifold $\A$

The printing operator $\Pi$ samples the access manifold $\A$ and deposits ringframe material $\rho$ into the time schema $\T$. It operates in distinct temporal modes—phasic, compressed phasic, interrupt, and extrusion—that determine how $\A$ is sampled over time.

2.9 Mic Signal ($\M$), Voice ($\vec{C}$), and Baseline Rhythm ($\beta$)

The printing operator $\Pi$ is primarily driven by the high-level mic signal $\M(t)$, guided by the aboutness vector $\vec{C}(t)$, and sustained in silence by the baseline rhythm $\beta(t)$.

• Mic signal $\boldsymbol{\M(t)}$: A transient, structured drive carrying any high-level events of consciousness. $\M(t)$ modulates the printing operator $\Pi$, producing organized ringframes that embody current goals, percepts, or thoughts. It is the amplitude envelope (if present) of any active "voice" aboutness vector (if present).
• Voice (aboutness vector $\boldsymbol{\vec{C}(t)}$): A directional vector in concept space that is what $\M(t)$ and $\beta(t)$ are about. $\vec{C}(t)$ governs what the system is about, biasing both $\M(t)$ and $\beta(t)$ toward the appropriate conceptual or perceptual surface within $\D$.
• Baseline rhythm $\boldsymbol{\beta(t)}$: An endogenous oscillation emerging from refractory dynamics, maintaining access continuity when $\M(t)$ is quiescent. $\beta(t)$ provides the rhythmic substrate on which $\M(t)$ rides, filling silent periods with spontaneous prints that preserve temporal coherence in $\T$. $\beta(t)$ provides a silent, slow (2–7 Hz) frame rate of dream and daydream imagery (which may also use $\M(t)$).

In concert, $\M(t)$ provides structure, $\vec{C}(t)$ supplies intent, and $\beta(t)$ sustains a minimal frame rate—together orchestrating the ongoing printstream of consciousness.

2.10 Observer Cameras ($\Xi_{\text{Cyclopean}}$, $\Xi_{\text{Mind's Eye}}$)

The two conscious viewpoints are modeled as infinitesimal point cameras with full $\mathrm{SE}(3)$ freedom. $\Xi_{\text{Cyclopean}}$ represents the fused avatar or "real" eye within $\R$, while $\Xi_{\text{Mind's Eye}}$ represents the internally oriented "imaginal" eye within $\I$. Each camera defines a right-handed coordinate frame with orthonormal basis vectors for gaze, up, and left:

Together, these provide the perspective impingement operators through which the $\R$ and $\I$ are viewed within the conscious display $\D$.

3 Physics Modeling, Schema/Camera Posing, and Perspective

The conscious display $\D$ (or $U_{\text{struct}}$) integrates three geometric streams: Physics—the inferred 3D world in $\R$; Perspective—the $\mathrm{SE}(3)$ camera pose; Pose—the $\Sim(3)$ overlay of Bank and Imaginal schemas. These determine what is seen, from where, and how internal volumes are scaled and placed.

3.1 Physics Modeling and Schema/Camera Posing

In computer animation, object physics (an apple falling) and camera scene-framing (orbiting around it) are separate elements jointly linked by keyframes. Similarly, the brain must reify raw signals into physical geometry, position the self-model at a viewpoint, and "pose" the overlay of mental imagery at a specific location, orientation, and scale (the posing is a Sim(3) action on $\I$). Finally, any ongoing aboutness stream is able to exert coordinated modulation on baseline behaviors (of bank, imagination, printing operator timing/modes, selection of $\A$, behavior output, etc.). The conscious display $\D$ (equivalently $U_{\text{struct}}$) is the integrated result of baseline defaults and any coordinated modulation by the aboutness vector $\vec{C}(t)$. The posing of $\B$, $\I$, $\Xi_{\text{Cyclopean}}$, $\Xi_{\text{Mind's Eye}}$, etc., are governed by a small set of Lie groups acting on Euclidean space, shown in Table 1.

$\Sim(3)$ sets global placement; $\mathrm{SE}(3)$ moves cameras within posed spaces. A radiance sphere $L(\omega,\nu)$ describes physical input, while $L_{\text{perc}}(\omega)$ encodes solved perceptual color/intensity per direction, shared by $\R$ and $\I$.

3.2 Camera Perspective (Radiance)

In addition to geometric transformations, the radiance sphere $L(\omega,\nu)$ represents the directional and frequency-dependent energy distribution over the unit sphere of orientations $\omega \in \mathbb{S}^2$ and spectral domain $\nu$. This quantity captures the angular structure of visual illumination and serves as the input to derive painted detail (paint) within the posed $\R$ schema.

Perceptually, the 2-D visual field of $\R$ or $\I$ consists of a single color (derived from a 3D opponent-color manifold of H/S/B) and intensity for any solid angle $\omega$.

$L_{\text{phys}}$ is the physical spectral input, while $L_{\text{perc}}$ is the unified perceptual radiance field for both externally grounded and internally generated scenes ($\R$ and $\I$). The Cyclopean and mind's eyes can each be modeled as infinitesimal point cameras embedded in the conscious display, possessing full $\mathrm{SE}(3)$ freedom with defined up, gaze, and left vectors for capturing perspective views from $\R$ and/or $\I$.

1. The spatial inverse problem: the eyes receive two-dimensional radiance patterns, yet the system must reify a three-dimensional world as their cause. Each retinal image is an array of directions $\omega$ whose depth structure must be inferred as reified source/altering objects within the real schema $\R$.
2. The color inverse problem: light from a distal surface (e.g. brown wallpaper) may pass through multiple semi-transparent layers—such as two layers of green glass from a Coke bottle and two of a red balloon—before reaching the eyes. V1 arrives at a single mixed color and intensity for that direction, yet the visual system must recover and assign distinct colors to the reified objects responsible for the mixture: the red balloon, the green Coke bottle, and the brown wall. This is analogous to cel animation rendered in three dimensions: each layer (wall, Coke bottle, balloon) contributes to the final pixel but retains its own object-attached color property in the reconstructed scene.
3. Perspective color vs. object color: in the conscious display, each viewing direction $\omega$ carries only one apparent color and intensity; but in the reified real schema $R$, multiple voxel locations along that ray—sometimes five or more—each possess their own color property anchored to object meaning and depth.

4 Aboutness Modulation and Multidimensional Control

The Bank $\B$ operates under rhythmic baseline behaviors (stationary, revolving, or ebb/flow), which maintain ongoing $\Sim(3)$ motion and spatial coherence. Superimposed upon these baselines is a multidimensional modulation envelope governed by an aboutness vector $\vec{C}(t)$ that coordinates pose, timing, and access across all active schemas.

4.1 Bank Baseline Behaviors and Modulation Envelope

• Stationary: Fixed $\Sim(3)$ pose requiring explicit $\T$ schema stabilization.
• Revolving (primary): Continuous $\Sim(3)$ motion with toroidal geometry—manifesting as pure rotation, spirographic rolling, or tidally locked orbit—with major radius ranging from compact (tight spirograph) to extended (torus-scale) trajectories. Cylinder, sphere, and cone variants of spirographic behavior may occur.
• Ebb/Flow: Hybrid oscillation combining slow scale-shifts with rapid inertial jerks.

These baselines are continuously deformed by a modulation envelope acting through three control domains:

4.2 Coordinated Aboutness Field

Aboutness is represented by a vector $\vec{C}(t)$ in concept space, but functionally behaves as a global control field synchronizing multiple geometric systems. It jointly modulates:

• The $\Sim(3)$ pose of the Imaginal schema $\I$ (scale, 3D orientation, and translation);
• The $\Sim(3)$ pose of the Bank $\B$, adjusting the reference geometry.
• The selection of the access manifold $\A$, which also fixes the effective $\Sim(3)$ pose of $\T$, and the timing of operations by $\Pi$.
• The mode and signal of the printing operator $\Pi$ (phasic, compressed phasic, interrupt, or extrusion), determining how ringframes $\rho(t)$ materialize in $\T$.
• The head/eye turns of the avatar (and of the mind's avatar, when present as a non-servo, pretend body schema in $\I$), and orbits, jumps, and other exotic behaviors of the mind's eye. All of these are examples of dynamic SE(3) posing of head and $\Xi_{\text{Cyclopean}}$ and $\Xi_{\text{Mind's Eye}}$.
• Jump-cuts and orbital cross-fades between $\R$ and $\I$ (as facilitated by $\Xi_{\text{Cyclopean}}$ and $\Xi_{\text{Mind's Eye}}$), and varying opacity overlays of $\I$ visible to $\Xi_{\text{Cyclopean}}$.

Thus, $\vec{C}(t)$ orchestrates simultaneous modulation across all these manifolds, binding pose, access, and printing into a unified act of reference.

4.3 Capture Dynamics and Timescales

Capture timescales:

• Short-term (Keyframing): Rapid modulations (100–500 ms) in "mic voice" (aboutness) — e.g., hand gesture shifts, driving gaze changes, cooking task transitions.
• Long-term (Locked capture): Sustained alignment (seconds) — e.g., tracking an object, watching a performer, or following a melody.

4.4 Unified Control Formulation

Baseline dynamics integrate with aboutness-driven modulation as:

4.5 Unified System Dynamics

The overall system evolves under dual influences: aboutness-driven modulation versus attractor-state inertia:

where $F$ describes $\vec{C}(t)$–driven coordination across all schemas and cameras, and $H$ denotes the system's tendency to maintain its current coupled configuration. $\alpha$ and $\gamma$ weight novelty versus habit.

4.6 Operational Examples

• Popcorn stand: scent $\rightarrow\vec{C}$ = popcorn location $\rightarrow$ $\B$ orients + scales + $\A$ walks.
• Street performance: visual salience $\rightarrow\vec{C}$ = juggler $\rightarrow$ long-term general capture, fast-moving balls may capture more transiently.
• Driving: $\vec{C}$ cycles: road $\rightarrow$ mirror $\rightarrow$ speedometer — keyframed attention.
• Daydream: $\vec{C}$ = imaginal surf scenario $\rightarrow$ extended internal capture.
• "Throw" (acceleration aboutness): A driver turns sharply to the left. This is rendered in $\D$ as the throw of $\A$ and $\B$ rightward and/or upward in $\R$.
• "Vibes" (amplitude envelope aboutness): The loud cymbal crashes of a song, or the texture of a violin note, modulate some facet (radius, frequency, attitude, intensity) of $\A$ in $\R$.

Aboutness, then, is not merely attentional bias but a coordinated multidimensional modulation linking $\B$, $\I$, $\A$, $\T$, $\Pi$, and the observer cameras into one temporally bound act of conscious reference. In hypnagogia—when wakeful control slips and sensory gating relaxes—aboutness can drive $\I$ so completely that its geometry and paint are experienced as real. Aboutness is likely capable of recruiting veridical imagery patterns in early visual cortex (V1), consistent with recent decoding evidence showing that imagined content evokes V1 activity indistinguishable from real visual input in phantasic individuals [9], suggesting that retinotopic, stimulus-like activation of V1 correlates with the presence and degree of perceptual "paint," even when abstractly driven from top-down, and even if the final correlate of conscious perception resides higher in the cortical hierarchy.

5 Access and Printing Modes

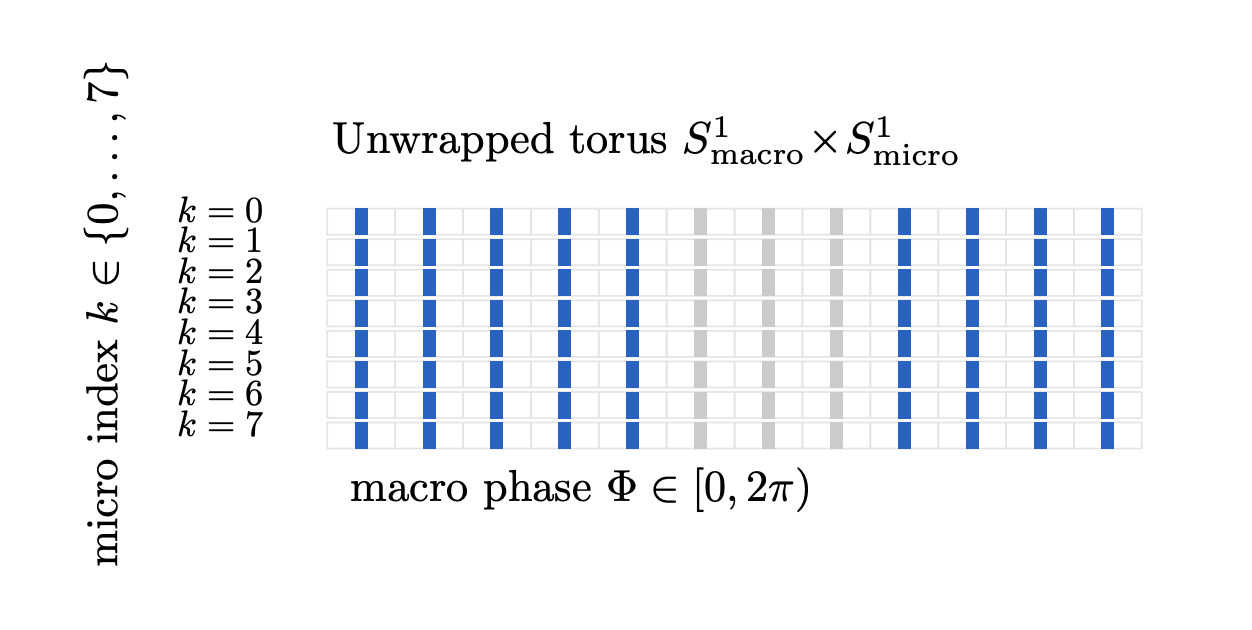
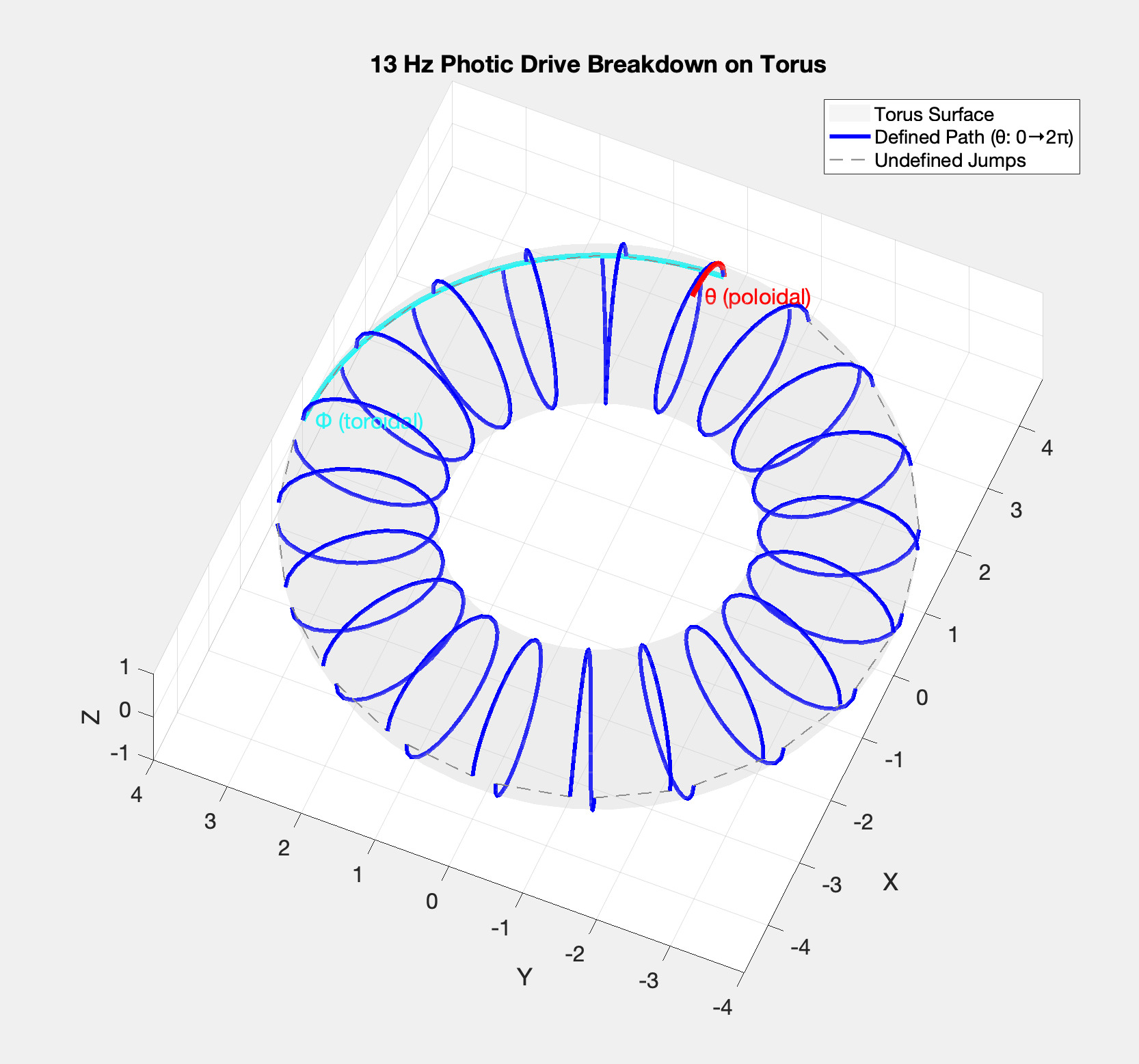
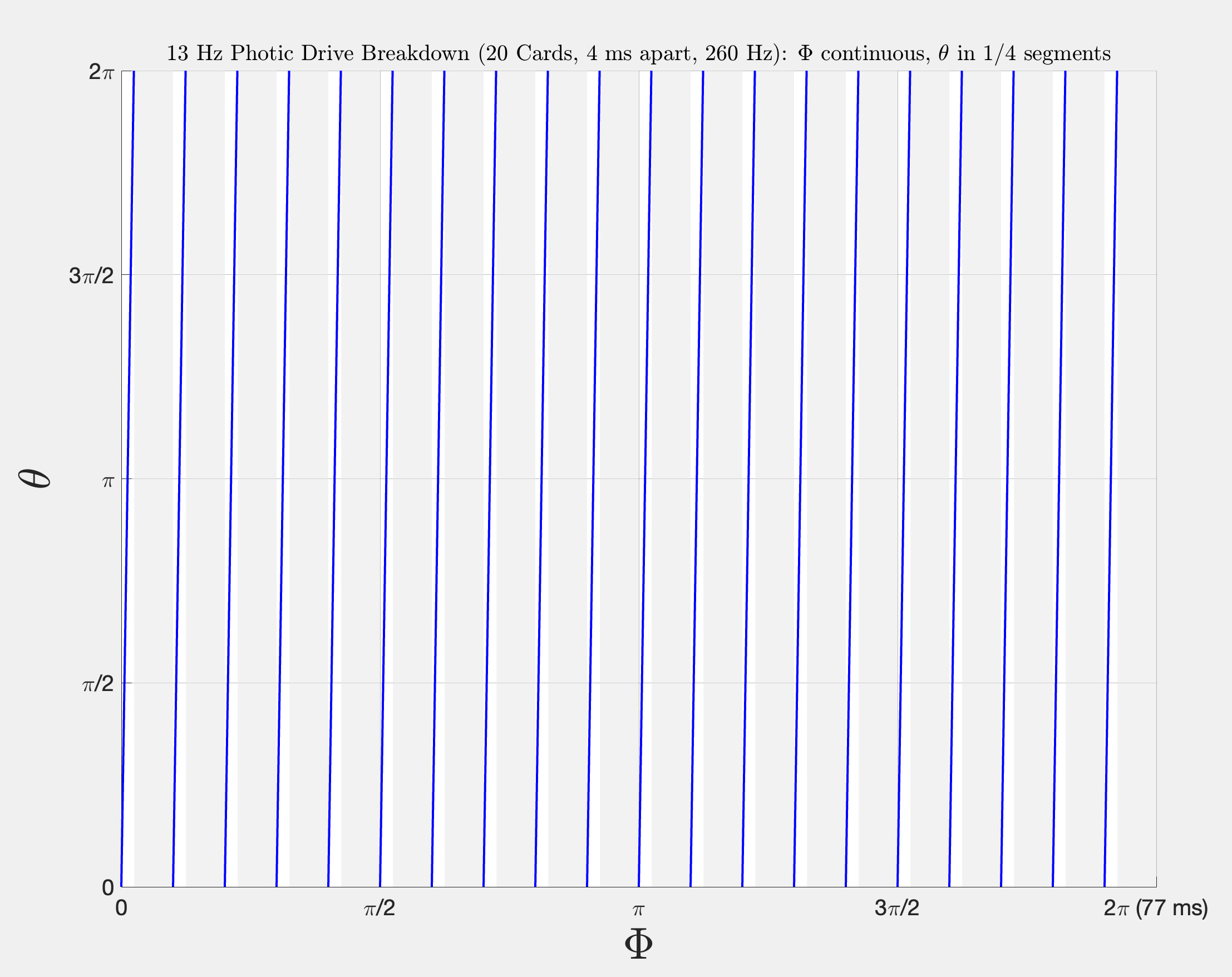
Let $\theta \in [0,\, 2\pi + \varepsilon)$ parameterize a local card/perimeter $\A$, where $\varepsilon > 0$ denotes a transient overshoot characteristic of compressed phasic motion. Define the active-phase set $\Pi(t)\subseteq[0,2\pi)$:

These modes appear at any scale (micro/local vs. macro/global) and can nest, e.g., a smooth global carrier with local interrupt "cards." "Rolodex" arises from tidally-locked orbital or rotational macrocycles hosting interrupt microcards (another name for ringframes $\rho$).

6 Hazard-Gated Timing

Interrupt scheduling follows a point-process hazard

with baseline $\beta(t)$, mic events at times $t_i$ with salience $\alpha_i$, event kernel $k(\cdot)$, and adaptation $a(t)$. Likelihood and survival follow standard point-process form; Ogata thinning simulates exactly. Photic entrainment elevates visual hazards selectively; non-visual channels can run in parallel. In phasic regimes, $\beta(t)$ and $\M$ modulate trajectory rather than gate.

7 Semiosis Cascade

RBT recasts Peircean semiosis as a three-stage temporal cascade:

1. Perceptual: mic/baseline (representamina) $\rightarrow$ prints $\rho$ on $\A$ (interpretant) $\rightarrow$ proto-object.
2. Cognitive: proto-object drives $\R/\I$ reconstruction (interpretant), yielding object-level content.
3. Metacognitive/action: $\R/\I$ becomes representamen for threat/affordance interpretation, shaping behavior (object) [6].

8 Neural Correlates and Predictions

Hyperpolarization bottleneck. Dissociative states exhibit slow ($\sim 2$ Hz) envelopes with fast bursts ($\sim 80$ Hz) [7,8]. RBT predicts interrupt-dominant access with long gaps, global cards per slow crest, and gamma bursts as print signatures.
Motor/temporal rings. Latent rotational trajectories in motor cortex and timing tasks map onto ringframes and card cadence [10,11].
Photic entrainment. 10–13 Hz strobe locks visual-plane access; fainter in-between cards (260 Hz) may appear (possibly by staggered max frequency, which may be capable of that staggered resolution, akin to premotor cortex).
Cardiac-phase gating. Heartbeat-coupled mic events bias hazard $h(t)$, altering interrupt likelihood.
Vestibular "throw." Transients shift pose via $\Sim(3)$ perturbations, briefly re-siting $\A$ for re-lock.

Empirical program: EEG beta/gamma power crests synchronized with musical transients [5].

9 Methods Sketch for Testing

1. Point-process modeling of frame events: infer $h(t)$ from discrete "card" times (blink-aligned, saccade-aligned, photic-locked), compare baseline-only vs. +mic vs. +adaptation models.
2. Dual-plane refresh: separate an attentional plane (slow) from a content plane (fast) via cross-frequency nested rate analysis.

10 Phenomenology Snapshots

Abortive wave. A global interrupt upon eye closure: $h(t)$ spikes, $\A$ prints against a black input, $\R$ fails to assemble rich paint; a turbulent ripple passes over the visual field plane.

Overexposure wave. Sudden bright entry causes a saturated print; the visual plane momentarily destabilizes under extreme luminance before re-stabilizing.

Gross$\to$fine. A half-second chirp from $\sim 4\rightarrow 40$ Hz prints successive geometric refinements (low to high geometric frequency; e.g., spatial frequency in 3D); color/paint arrives late [2].

Dissociation. Strong slow baseline with a transient, seconds-long anticorrelation of phase of brain regions may correlate with "true" dissociation (metacognition detaches from control of avatar in $\R$ and becomes observer-only).

11 Acknowledgments of Prior Observations

Carl Sagan's "Mr. X" imagery suggested outlines-first semiosis: "outlines of...instant appreciation" seems to describe $\R$ magically appearing from the operation of $\Pi$ on $\A$ [6]. Lehar described cyclic gross$\to$fine rendering and concentric scaffolds [2,3]; see also Cube Flipper's exegesis [12]. Our prior EEG results showed beta/gamma power aligned to musical transients consistent with access gating [5].

12 Conclusion

RBT frames conscious semiosis as the geometry and timing of access followed by conceptual understanding. The Bank $\B$ (posed by $\Sim(3)$), the Access Manifold $\A$, and the printing operator $\Pi$, together deliver ringframes $\rho$ into the Time Schema $\T$ (guided by $\vec{C}$, driven by $\M(t)$ and $\beta(t)$), from which $\R$ and $\I$ are read out with latency. Baseline dynamics establish cadence; aboutness modulation steers pose/walk/timing to bind "what matters now." The hazard formalism unifies phasic modulation and interrupt gating, connecting phenomenology to testable neural signatures across normal, entrained, hyperpolarized (sedated), and anesthetized states. Hyperpolarization is thought to collapse distributed bank usage into a single embodied stream of phenomenology: as membrane potentials drift downward and NMDA-dependent excitation weakens, beta/gamma activity vanishes, and cortical dynamics become globally entrained—first around the alpha range (∼10 Hz), then slowing into delta during deep sedation (2–4 Hz), and finally into ultra-slow oscillations near 1 Hz under anesthesia, where multiplexed access effectively ceases.

Symbol/Notation Glossary

• $\B$: Bank (shape manifold), $S\in\mathcal{S}$ modulo translation/rotation/scale.
• $\Sim(3)$: similarity group (scale $s>0$, $R\in\SO(3)$, translation $t\in\mathbb{R}^3$).
• $g(t)\in\Sim(3)$: pose/scale action placing $S$ for display.
• $\A(t)\subset X_{\mathrm{display}}(t)$: Access Manifold (local $0$–$2$D).
• $\rho(t)=\Pi(\A,S,g)$: ringframe printed into $\T$.
• $\T$: Time Schema (fading buffer/flowfield).
• $\R,\I$: Real/Imaginal readouts reconstructed from recent $\rho$ and context.
• $h(t)$: hazard (instantaneous print likelihood); $\beta(t)$: baseline cadence; $a(t)$: adaptation.

Bank $\B$: a shape in Kendall space posed by $g(t)\in\Sim(3)$ (scale, rotation, translation).

Operational intersection vs. structural union: multiple 3D schemas form $\Ustruct$; conscious sampling occurs on the $0$–$2$D access manifold $\A(t)$ ($\A$ is here labeled "union set," as in the shared, intersecting voxels between all schemas) (models from [13,14]).

(a) Clear hemishell with frame triad (gaze, up, left)

(b) Painted hemishell with colored ray-rods

Incoming light is modeled as straight rays converging at the pupil. (a) A viewing-frame triad within a clear hemispherical dome. (b) A painted hemishell on $\mathbb{S}^2$ illustrates directions $\omega$ for $L_{\text{phys}}(\omega,\nu)$ and $L_{\text{perc}}(\omega)$. Real and mind's eye cameras [$\Xi_{\text{Cyclopean}}$, $\Xi_{\text{Mind's Eye}}$] have $\mathrm{SE}(3)$ freedom within posed $\R$ and $\I$.

Global "all-hot" spirographic mode: the entire bank shell is active and moves as a unit under $g(t)$.

Continuum of access: phasic $\rightarrow$ compressed phasic $\rightarrow$ interrupt.

(a) Radial history gradient view	(b) Pure skewer geometry
(c) Cross-section through bank	(d) Letter "b" skewer pathway

Radial History Stack (Bank Skewer $\B_{\mathrm{Sk}}$): Content instances organize radially: present (outer) to past (inner). (a) Temporal gradient view; (b) Pure skewer geometry; (c) Cross-section through bank; (d) Letter "b" pathway. Enables overview of concept history when $\A$ prints nearby, supporting serial dependence and emotional pathway following. Skewer itself inferred; chasm/layers phenomenologically accessible but typically subconscious due to rapid printing, $\R$ dominance, and latch-on to most recent case.

Horizontal torus: 3D macrocycle with tangent-facing microcycle "cards." Pattern: $M{=}8$, $B{=}5$ bright and $3$ dark.

Macro$\times$micro torus (unwrapped, blip rendering). One macrocycle ($T_{\mathrm{macro}}$) with $M{=}8$ micro slots; pattern $B{=}5$ bright, $3$ dark. Each slot shows a brief blip (bright or dim) with silence for the rest of the slot—matching interrupt-like micro-prints or compressed-phasic micro sweeps whose active fraction $d=\tau/T$ is small and hazard/adaptation-modulated.

Vertical (sagittal) torus ("paddlewheel"): In this mode, the access manifold is a card-like plane (or its perimeter) carried around a 2-s macrocycle. It turns hot only in brief blips, spaced $\sim$250 ms apart (4 Hz), a pattern typical of hypnagogia as beta/gamma power wanes and global theta–delta entrainment rises. Each theta/delta crest corresponds to printing one card: upper-sector (bright) cards broadcast imaginal content; lower-sector (dim) cards lightly interface with the Real schema as the mic line shuts down and the baseline rhythm sets the dream frame rate. Timing: per-card perimeter microcycle $\tau_{\mathrm{micro}}\!\approx\!10$ ms (near-instant sweep), inter-card period $T_{\mathrm{micro}}\!\approx\!250$ ms, macrocycle $T_{\mathrm{macro}}\!\approx\!2$ s.

Photic Drive Breakdown: Under 13 Hz strobe entrainment, $\B$ (and thus $\A$) rotate in a tidally locked orbit. In light hyperpolarization, the "paint" flash may fragment into $\B$ revolving 13 times per second, printing one bright flash-card per revolution and leaving a trace of higher-frequency ($\sim$260 Hz) dark cards. Roughly 20 cards are produced per revolution, implying spatial–temporal precision of $\sim$200 $\mu$s in modeling space.

Unwrapped Breakdown: As $\tau \!\rightarrow\! 0$, each card's local $\theta$-phase compresses into a near-instant blip, leaving most of the card-to-card microperiod $T$ silent or passive.

Global mode example (shown as compressed phasic): A macrocycle contains a compressed active phase $\tau$ within a larger period $T$ (major circle of the torus). A hot plane—locally in extrusion mode—completes one revolution during $\tau$, then holds its pose for the remainder of $T$ ($\tau < T$).

Bibliography